On peut réaliser l’expérience des hémisphères de Magdebourg avec deux verres ou deux ventouses de caoutchouc.
Fiche d’accompagnement de l’expérience:
 Matériel
Matériel- 2 verres identiques avec un bord aussi lisse que possible
- du coton et de l’alcool à brûler ou bien une toute petite bougie
- un bout de papier essuie-tout
- accessoires : des allumettes ou un briquet
ou bien
- 2 ventouses de caoutchouc ou à défaut une seule
 Montage et réalisation
Montage et réalisationMouiller un morceau de papier essuie-tout.
Imbiber d’alcool à brûler un morceau d’ouate et l’enflammer.
Le jeter dans un verre, couvrir immédiatement le verre avec le papier et placer le deuxième verre renversé sur le premier, en faisant coïncider exactement leurs bords (voir la figure). Quelques secondes après que la flamme se soit éteinte, on constate que les verres restent « collés » l’un à l’autre : on peut soulever les deux verres ensemble en ne saisissant que celui du dessus.
On peut remplacer le coton imbibé d’alcool par une petite bougie.
Placer la bougie dans l’un des verres et l’allumer.
Poursuivre alors l’expérience telle qu’elle est décrire ci-dessus.
On peut aussi utiliser deux ventouses de caoutchouc pour réaliser un modèle expérimental des hémisphères de Magdebourg.
Après les avoir pressées l’une contre l’autre comme sur la figure précédente, on se rend compte qu’il faut exercer une très grande force pour les séparer.
Si l’on ne dispose que d’une seule ventouse il suffit de la presser contre un mur carrelé.
 Explications
ExplicationsDans toutes ces expériences, qu’il s’agisse des hémisphères historiques, des deux verres ou des ventouses, on réalise une dépression à l’intérieur du dispositif (voir plus loin).
La pression atmosphérique  qui règne à l’extérieur est supérieure à la pression
qui règne à l’extérieur est supérieure à la pression  de l’air à l’intérieur.
de l’air à l’intérieur.
Pour simplifier, nous négligerons la variation de pression avec l’altitude.
Considérons un seul hémisphère : il peut être décomposé en parallélépipèdes rectangles élémentaires qui sont représentés très schématiquement en coupe sur la figure suivante (les grandes lignes de la justification mathématique se trouvent dans le paragraphe « Remarques »).
L’hémisphère peut avoir une forme quelconque. Soit A la valeur de la section plane, de vecteur surface  , s’appuyant sur les bords de l’hémisphère. Le deuxième hémisphère n’est pas représenté sur cette figure pour éviter les surcharges.
, s’appuyant sur les bords de l’hémisphère. Le deuxième hémisphère n’est pas représenté sur cette figure pour éviter les surcharges.
Chaque élément de surface  de l’hémisphère est soumis à une force pressante
de l’hémisphère est soumis à une force pressante  , perpendiculaire à l’élément de surface et dirigée vers l’intérieur, qui résulte de la différence de pression entre l’extérieur et l’intérieur :
, perpendiculaire à l’élément de surface et dirigée vers l’intérieur, qui résulte de la différence de pression entre l’extérieur et l’intérieur :

La résultante de ces forces élémentaires a pour composante suivant l’axe x :
 (voir la figure précédente).
(voir la figure précédente).
Finalement,  car
car  .
.
La résultante de ces forces élémentaires a pour composante suivant l’axe y :
Fy = Sb(patm – pi) – Sh(patm – pi) = –A(patm – pi)
(indices « g » pour gauche, « d » pour droite, « b » pour bas et « h » pour haut).
La force résultante  est donc perpendiculaire à la section plane fictive s’appuyant sur les bords de la ventouse et elle est dirigée vers l’intérieur de l’hémisphère (voir la figure ). Elle a pour valeur :
est donc perpendiculaire à la section plane fictive s’appuyant sur les bords de la ventouse et elle est dirigée vers l’intérieur de l’hémisphère (voir la figure ). Elle a pour valeur :

Par un raisonnement analogue, on montrerait que l’autre hémisphère subit des forces pressantes dont la résultante  est opposée à
est opposée à  . Les forces
. Les forces  et
et  pressent les deux hémisphères l’un contre l’autre.
pressent les deux hémisphères l’un contre l’autre.
Expliquons maintenant comment apparaît la dépression entre les deux verres. Echauffé par la flamme, l’air situé dans le verre inférieur se dilate et s’échappe par-dessous le papier essuie-tout. Une fois que la flamme est éteinte, l’air du verre inférieur se refroidit, donc sa pression diminue. Le papier mouillé placé entre les deux verres joue le rôle d’un joint étanche qui empêche l’air extérieur d’entrer. Les pressions s’égalisent dans les deux verres car le papier, qui est poreux, laisse un peu d’air passer du verre supérieur au verre inférieur. La nouvelle pression à l’intérieur reste inférieure à la pression extérieure.
Lorsqu’on appuie les deux ventouses l’une sur l’autre, on comprime l’air situé dans l’espace intérieur et on augmente donc sa pression : sous l’effet de cette surpression, une certaine quantité d’air s’échappe. Comme les ventouses en caoutchouc sont élastiques, elles reprennent leur forme initiale lorsqu’elles ne subissent plus de force de déformation. Le volume de l’espace intérieur augmente alors, entraînant une diminution de la pression de l’air emprisonné. La pression de l’air intérieur étant inférieure à la pression atmosphérique, les ventouses sont soumises à des forces pressantes qui les rapprochent l’une de l’autre. Les bords des ventouses constituent des joints étanches. Comme l’air extérieur ne peut pas entrer, la dépression subsiste.
 Remarques
RemarquesLes hémisphères de Magdebourg originaux étaient deux demi-sphères de cuivre creuses, d’un diamètre approximatif de 42 cm, dont les bords s’adaptaient parfaitement sans laisser passer l’air. En 1654, Otto von Guericke (1602-1686) réussit à obtenir un très bon vide entre les deux demi-sphères. Pour les séparer, il fallut atteler 8 chevaux de chaque côté [Lenk 1989, p. 571].
On peut étayer les explications citées plus haut par une justification un peu plus théorique.
Les deux hémisphères placés bord à bord constituent une surface fermée S qui entoure le volume V. Chaque élément de surface  est soumis à une force pressante due à la différence entre la pression intérieure et la pression extérieure. On calcule la force résultante
est soumis à une force pressante due à la différence entre la pression intérieure et la pression extérieure. On calcule la force résultante  qui s’exerce sur S en utilisant le théorème de Gauss pour les champs scalaires :
qui s’exerce sur S en utilisant le théorème de Gauss pour les champs scalaires :
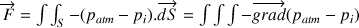
Comme  , on a
, on a  , ce qui donne
, ce qui donne  .
.
Il en résulte que si l’on coupe la surface S par un plan P, on obtient deux surfaces partielles  et
et  soumises respectivement aux forces pressantes résultantes
soumises respectivement aux forces pressantes résultantes  et
et  qui sont opposées (
qui sont opposées (  ).
).
Pour estimer la valeur commune de ces forces, faisons l’opération suivante : réduisons l’une des deux surfaces, par exemple  , à la section A entre S et le plan P. Il n’en résulte aucune modification pour la force
, à la section A entre S et le plan P. Il n’en résulte aucune modification pour la force  . Par ailleurs
. Par ailleurs  est opposée à la force
est opposée à la force  qui s’exerce sur la section A :
qui s’exerce sur la section A :

Puisque la section est plane, on calcule aisément :
 .
.
On retrouve bien ainsi le résultat énoncé au paragraphe précédent.

